「圆之源」还是「源之圆」，傻傻分不清。

若部分数学公式不能正常显示，可前往 这里(opens new window) 查看。

📋 目录

古希腊伟大的数学家毕达哥拉斯曾说：圆是一切平面图形中最美的图形. 然而在数学解题时，我们往往发现不了美丽的圆，因为很多时候圆是隐藏着的. “隐圆”，顾名思义，即为隐藏着的圆，发现“隐圆”不仅需要一双“发现美的眼睛”，更需要有扎实的数学基础. 本文以各类隐圆为例，发掘圆之源，探究其解法，领略圆之美.

# 一、圆的直径所对圆周角为直角

定义

众所周知，圆的直径所对圆周角为直角. 我们指出，其逆命题也成立，即在平面内给定两点 ，设点 在同一个平面内且满足 ，则点 在以线段 为直径的圆上，即点 的轨迹是一个圆，该圆的圆心为线段 的中点，半径 .

例 1（2014 年北京卷文第 7 题）已知圆 和两点 . 若圆 上存在点 ，使得 ，则 的最大值为

解答：由 知点 的轨迹为一个圆，易知其方程为圆 . 因为圆 上存在点 ，使得 ，所以圆 与圆 有交点，于是 ，解得 ，因此 的最大值为 ，故选 .

# 二、三角形的外接圆

定义

一般地，在 中，角 所对的边分别是 ，根据正弦定理， 外接圆直径

特别地，若 是以角 为直角的直角三角形，且 ，则 的外接圆方程为

例 2（2014 年全国 Ⅱ 卷文第 12 题）设点 ，若在圆 上存在点 ，使得 ，则 的取值范围是

解答：，由正弦定理知 的外接圆直径

又因为点 均在圆 上，所以

于是

故选 .

点评：本题关键之处是运用正弦定理求出的外接圆直径为定值，然后再根据线段的长度不大于外接圆直径建立不等关系，从而求出 的取值范围. 此解法巧妙地避开了对极限位置的讨论，准确而简洁.

例 3 已知椭圆 的左右焦点分别为 ，直线 过点 且垂直于椭圆的长轴，动直线 垂直于直线于点 ，线段 的垂直平分线与 的交点的轨迹为曲线 ，若 ， 是 上不同的点，且 ，则 的取值范围是

以上都不正确

解答：由抛物线定义知 的方程为

由题意知 的外接圆方程为

又 ，所以外接圆方程为

整理得

其判别式 ，即

于是 或

又 ，所以

于是 或 ，故选 .

# 三、勾股圆

定义

已知点 ，动点 ，若动点 满足 ，则动点 的轨迹为一个圆，其方程为

因动点 满足的式子类似于勾股定理，故称动点 的轨迹为“勾股圆”.

例 4 已知 ，点 是圆 上的动点，且满足 ，若满足条件的点 有两个，则 的取值范围是

解答：设点 ，则

于是

整理得圆

因为点 是圆 上的动点，且满足条件的点 有两个

所以圆 与圆 相交，所以

所以 ，故选 .

# 四、类蒙日圆

定义

众所周知，椭圆 的任意两条互相垂直的切线的交点在同一个圆上，这个圆叫“蒙日圆”，其方程为

特殊地，当椭圆 退化为圆 时，那么圆 的任意两条互相垂直的切线的交点也在同一个圆上，我们称之为“类蒙日圆”，其方程为

例 5 已知圆 ， 为圆 上一点，若存在一个定圆 ，过点 作圆 的两条切线 ，切点分别为 ，点 在圆 上运动时，恒有 ，则圆 的方程为

解答：易知圆 与圆 为同心圆，于是排除 选项. 可知圆 为“类蒙日圆”，因此圆 的半径为 ，所以圆的方程为 ，故选 .

例 6 设直线 ，圆 . 若在直线 上存在一点 ，使得过点 的两条切线 （ 为切点）满足 ，则 的取值范围是

解答：由题意知点 在圆 上

所以直线 与圆 有交点

于是

所以 ，故选 .

# 五、阿波罗尼斯圆

定义

古希腊数学家阿波罗尼斯（约公元前 262 — 前 190）在其著作《圆锥曲线论》中有一个著名的几何问题：在平面内给定两点 ，设点 在同一个平面内且满足

则点 的轨迹是一个圆. 我们称这个圆为“阿波罗尼斯圆”，简称“阿氏圆”.

例 7（人教 A 版教材必修二第 131 页练习题 B 第 3 题）已知一曲线是与两个定点 、 的距离的比为 的点的轨迹，求此曲线的方程，并画出曲线.

解答：设 是曲线上任意一点，则

整理即得该曲线的方程为 . 易知该曲线为圆心是 ，半径为 的圆.

例 8（2008 年江苏卷第 13 题）满足条件 的三角形的面积的最大值是___.

解答：

方法一：以线段 的中点 为原点， 所在直线为 轴，线段的中垂线为 轴建立平面直角坐标系，则 ，令 ，则

所以

化简得点 的轨迹方程为

可知在 中，当边 所对应的高 最大时， 的面积最大

又因为点 在圆 上，所以边 所对应的高的最大值为

所以

则三角形 的面积的最大值为 ，故填 .

方法二：如果纯粹从解三角形的角度来看这道题，就得到此题的常规解法：

设 ，则

根据三角形面积公式得

根据余弦定理得

代入上式得

由三角形三边关系有

\left\{\begin{array}{l}{\sqrt{2} x+x>2} \\ {x+2>\sqrt{2} x}\end{array}\right.

解得

故当 即 时， 的面积取得最大值 ，故填 .

点评：这是一道关于阿波罗尼斯圆的经典题目，乍一看与圆没有任何关系，然而其命题背景正是阿波罗尼斯圆，从命题者的角度来看，最好的解法一定是方法一而不是方法二. 通过两种解答方法的对比，我们可以看出，方法一对思维能力要求高，计算能力要求低，而方法二恰恰相反，对思维能力要求低，计算能力要求高，因此更容易出错. 高考命题要求“多想少算”，也只有“多想少算”，才能提高答题速度和准确率.

例 9 已知等腰三角形 腰上的中线长为 ，则该三角形面积的最大值为___.

解答：记等腰三角形 的中线与 交于点 ，不妨令 ，于是

以线段 的中点 为原点， 所在直线为 轴，线段 的中垂线为 轴建立平面直角坐标系

则

令 ，则

所以

化简可得

作图易得动点到直线距离的最大值为

于是可知 的最大值为

因此 面积的最大值为 ，故填 .

例 10（2013 年江苏卷第 17 题）如图，在平面直角坐标系 中，点 ，直线 . 设圆的半径为 ，圆心在 上.

（Ⅱ）若圆上存在点 ，使 ，求圆心 的横坐标 的取值范围.

解答：（Ⅱ）因为圆的圆心在直线 上

可设圆心 的坐标为 ，则圆 的方程为

因为

可设 ，则

整理得 ，设为圆

所以点 既在圆 上又在圆 上，即圆 和圆 有交点

所以

化简得

\left\{\begin{array}{l}{5 a^{2}-12 a+8 \geq 0} \\ {5 a^{2}-12 a \leq 0}\end{array} \Rightarrow 0 \leq a \leq \frac{12}{5}\right.

综上所述， 的取值范围为 .

# 六、立体几何中的圆

定义

立体几何中的一种重要思想方法就是“立几问题平面化”，即将三维的空间分解为二维的平面，使问题变得熟悉，从而更容易解决，这也体现了一种“一般与特殊”的思想. 因此立体几何中的圆也没有什么高深之处，只不过是从平面到了空间.

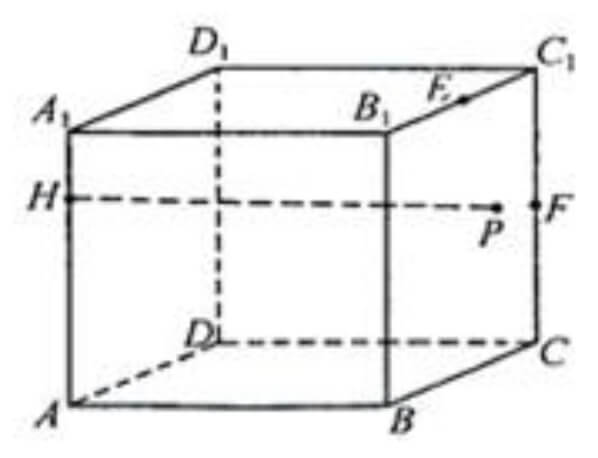
例 11（2015 年成都一诊文第 10 题）如图，已知正方体 的棱长为 ，点 在棱 上，且 ，点 分别为棱 的中点， 为侧面 内一动点，且满足 ，则当点 运动时， 的最小值是

解答：因为 ，所以点 在一个圆上，该圆的圆心为线段 的中点，半径

又点 平面 ，所以点 的轨迹是一段圆弧

过点 作 ，垂足为

可知 ，且

于是

在平面 内， 的最小值为

于是 的最小值为 ，故选 .

点评：本题的关键是对条件 进行转化，其本质为前文提到的第一类隐圆. 突破这个难点之后，本题也就没有什么难度了，接下来的问题就迎刃而解了.

例 12 已知平面 平面 ，且 ，平面 内两直线 均与 垂直，且 ，动点 在平面 内满足 ，则三角形 面积的最大值等于

解答：如图，根据题意得到

\left\{\begin{array}{l}{\alpha \perp \beta} \\ {\alpha \cap \beta=A B} \\ {D A \subset \beta, C B \subset \beta} \\ {D A \perp A B, C B \perp A B}\end{array} \Rightarrow D A \perp \alpha, C B \perp \alpha\right.

因为

\left\{\begin{array}{l}{D A \perp \alpha} \\ {P A \subset \alpha}\end{array} \Rightarrow D A \perp P A\right.

于是在直角三角形 中，

因为

\left\{\begin{array}{l}{C B \perp \alpha} \\ {P B \subset \alpha}\end{array} \Rightarrow C B \perp P B\right.

于是在直角三角形 中，

因为 ，所以 ，可知点 的轨迹为阿波罗尼斯圆的一部分

在平面 内，以线段 的中点 为原点， 所在直线为 轴，线段 的中垂线为 轴建立平面直角坐标系

可知

令 ，则

于是

化简得 ，易得动点 到直线距离的最大值为

所以 ，即三角形 面积的最大值为 ，故选 .

点评：本题是一道立体几何与解析几何相结合的题目，有一定的难度. 首先要用立体几何知识确定相关垂直关系，再在此基础上判断点的轨迹，最后用解析法求出三角形面积的最大值. 当然，在得到结论后，也可按照例 8 的方法二来求出答案，有兴趣的同学可以试一试.

# 参考文献

[1] 人民教育出版社课程教材研究所. 普通高中数学课程标准实验教科书数学 A 版必修二[M]. 北京: 人民教育出版社, 2007.

[2] 张森国. 以“阿波罗尼斯圆”为背景的考题探究(opens new window) [J]. 中学数学, 2015,(1):76-77.

[3] 叶柏团, 黄清波. 由阿波罗尼斯圆衍生圆锥曲线的优美性质(opens new window) [J]. 福建中学数学, 2016,(1):14-16.

# 学长瞎 BB

这篇文章是我在 2016 年暑假开始写的，由于各种原因，一直没有完成。但是现在这是一篇献给你们，也是献给我的高中的文章。2017 年 2 月 14 日我来到南山，恰巧《仙报姑》第一期完成（PS：我很疑惑为什么叫《仙报姑》而不叫《仙姑报》？）。看到贵刊面向全国征稿，于是我就来投稿了。希望 2017 级 2 班同学都能参与到《仙报姑》的编写创作中，这样既能巩固数学知识，增强对数学的兴趣，又能留下美好的高中回忆。

关于文章内容，不完善之处在所难免，吸收对自己有用的即可。如果觉得没用或者作业太多时间不够，就看看表情包笑一笑吧，毕竟做人最重要的是开心嘛。对于其中的点评内容，你们看看就好，不必太当真。因为我比较喜欢用表情包表达心情，所以文章中加入了一些表情包，但是我不知道你们能不能理解我想表达的意思（他们说我的想法有点奇怪），不能理解之处，意会就好。如果有想与我探讨 数学 表情包的同学，欢迎找我交流哦～

当然，在此还要特别感谢我们的何仙姑，感谢仙姑将数学讲得如此之好，对待学生如此真诚。向仙姑学习的不仅是他对待数学的态度，更是他对待人生的那一份率真与坦然。

最后，用 数学日历(opens new window) 中的 7 日、8 日、22 日这 3 个日期来祝福大家，希望大家的 2017 年 6 月 7 日和 8 日都能像日历中的 7、8 日一样美妙，在 6 月 22 日晚上带着 15 兼 16 级学长（也就是我）的双重祝福查出自己感觉都配不上的分数。真诚地祝福大家 2017 高考大捷，都能进入自己理想的大学！加油吧，少年！